Energy use in Buildings – Sustainable Energy – TU Delft
How much energy does my home need? After looking at the energy use in transportation in the last lecture, we will now turn our attention to the energy use in our buildings and homes. How does a house use energy? The largest share of the energy used in any house or building, is used in heating or cooling the indoor air. If it is very cold outside, we need to raise the temperature inside our house and prevent the indoor heat from escaping. Correspondingly, if it is very hot outside, we need to cool our houses and prevent the heat from entering the house. Cooking also requires a significant amount of energy and is an expense we cannot avoid!
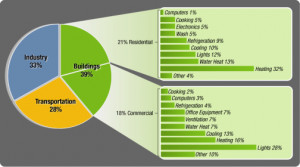
Additionally, there are several energy-intensive electrical appliances in our homes today. Lighting, an important part of every indoor environment, often consumes less energy than other electric appliances. Heating or cooling anything – air, water, or food – is an energy-intensive process and as such, appliances related to heating or cooling are often energy-intensive. Air conditioners and space heating appliances have a very large power requirement, as do cooking ovens, toasters and microwaves. It should be noted that appliances like the blender, steam iron and toaster are only used for a small time interval. This reduces the energy used when compared to appliances like the air conditioner, which are used for a much longer duration. Let us now look closer at the largest domestic energy requirement – space heating and cooling.
The energy required for space heating or cooling can be significantly reduced by wisely choosing the wall and the window material, and the architecture of the enclosed space. Let us consider a brick-walled room, with a glass window. It is a hot day and the outside temperature is T-O, while the room is at a lower temperature of T-i. The heat energy from the outside air will be passed through the walls and windows to the inside of the house. The energy is transferred by vibrations of neighboring molecules in the wall and windows. This leads to an increase in the indoor temperature. This mechanism of heat transfer is called conduction, denoted by Q-c. The power transferred through conduction is given by the expression, Q-c equals lambda times delta-T divided by d, multiplied by A. Here, lambda is called the thermal conductivity of the wall, delta T is the temperature difference between the outdoor and indoor air, d is the thickness of the medium, and A is the surface area of the wall or the window through which conduction occurs. This expression can also be rearranged: Lambda divided by d, is known as k. k is the thermal conductivity for the material through which conduction occurs. Q-c can thus be re-written as k times delta-T times A. The inverse of the thermal conductivity is expressed as R, which is called the thermal resistance of the material in question. The thermal resistance is a material property and can be used to calculate the heat transfer through different connected media. Let us assume that the room has a double-paned window. There are two panes of glass with thickness d-g separated by a d-a thick layer of air. The thermal resistance of the window can then be obtained by adding the individual thermal resistances, just like adding electrical resistances in series.
The total resistance of the double-paned glass can thus be calculated. Heat transfer also occurs via convection, denoted by Q-w. Heat transfer at a surface by convection is the transport of thermal heat from the solid to a flowing of gas or liquid, or the other way around. It is expressed as h times delta-T times A, where h is the heat transfer coefficient for convection, delta-T is the difference in temperature between the wall and the indoor air temperature, and A is the relevant wall surface area. It is important to note that in convection, the temperature of the wall T-w is used for calculating delta-T instead of the outside air temperature T-o which we used for conduction. As before, the inverse of the heat transfer coefficient is called the thermal resistance to convection, denoted by R-conv. The thermal resistances for conduction and convection can both be added together to give the total thermal resistance of the material, in this case the wall. Knowing the k and the h values of the wall material, the heat transfer through the wall can be calculated. The overall heat transfer coefficient U is 1 divided by the overall thermal resistance, R_wall_total, and has the unit Watt per square meter Kelvin. The heat transfer to a solid wall is mainly limited by the thermal resistance of the solid parts; the heat transfer through a window is limited by the heat transfer to and from the surfaces. Apart from conduction and convection, heat transfer also takes place through a mechanism called radiation. However, for the temperatures that we encounter in our homes, the heat transfer through radiation can be neglected and is therefore be ignored.
Another heat transfer mechanism that we do encounter in our homes is ventilation, denoted here by Q-v. The heat transfer through ventilation, Q-v is equal to m times C-p times delta-T, where m is the mass of air exchanged per second, C-p is the specific heat capacity of air, and delta-T is the difference in temperature between the outdoor and indoor temperature. All these three equations implicitly assume that the indoor and the outdoor temperatures, and the temperature of the wall stay constant throughout the heat transfer process. In reality, the indoor temperature will increase due to heat transfer through the walls leading to more complex equations. Let’s look at an example for thermal conductivity and convection. The outside temperature is 30 oC and the inside temperature is 20 oC which means we have a temperature difference of 10 oC. We will consider a double-paned window of 10 square meters in a relatively warm country. The thickness of the single glass windows are 3 mm and the thickness of the air gap between the glas is 1 cm. To calculate the total thermal power leaking out of this window we need to consider both the thermal conductivity of the glass and air gap, and the thermal convection at the outside and inner surface.
Typical thermal conductivity of glass, lambda-g, is 0.96 W per meter Kelvin and of air, lambda-a, is 0.024 W per meter Kelvin. A typical value for the external heat transfer coefficient for convection is 23 W per square meter Kelvin, whereas a typical value for the internal heat transfer coefficient for convection is 8 W per square meter Kelvin. With these numbers we can calculate the effective thermal resistance of the double-paned window using the discussed equations. As you can see, we arrive at a thermal resistance of 0.59 square meter Kelvin per Watt. The overall heat transfer coefficient U of the double-paned window is one divided by the total thermal resistance and is equal to 1.69 W per square meters per Kelvin. So we can calculate the total thermal power loss through the double glass window of 10 square meters. This is 169 W. To demonstrate the effect of thermal insulation of double windows in reference to single glass windows, we make the same calculation for the latter case. Here we arrive at an overall heat transfer coefficient U of 5.8 W per square meters Kelvin. For a single glass window of 10 square meters we have a thermal power loss of 583 W. Going from double glass to single glass increases the thermal power loss more than a factor of three! Let’s look at an example for transfer of thermal energy due to ventilation of a typical house in similar conditions. Outside temperature is 30 oC – inside temperature is 20 oC.
The total volume of the house is 100 cubic meters. A typical volume flow for ventilation is 30 liters per second or 0.03 cubic meters per seconds. This means that within 56 minutes all air in the house is replaced by new air from the outside. Taking the specific heat of air of 1005 J per kilogram Kelvin, an air density of 1.2 kg/m3, total thermal power flux into the house is 363 Watts. Let us now take a look at our household electricity use, and how it differs for different parts of the world. People living in the United States have one of the highest per capita household electricity usage at 12 kilowatt-hours per person per day, while people in India use only 0.5 kilowatt-hours per person per day. This is due to not only a difference in average standard of living and total population, but also a vast difference in access to electricity. If the access to electricity is taken into account, the average electrified household in India consumes about 2.9 kWh compared to 33.7 kilowatt hours in the United States. This table splits this electricity use up into the energy requirement for space heating and cooling in the green column, and other electrical appliances in the orange column. Assuming an average of 3 people per electrified household, we get the electricity use per person per day for the different parts of the world. Countries with a higher standard of living, as well as a colder climate have space-heating taking up a much larger share of their household energy consumption. Can you estimate how much energy your house uses every day? At the end of the last lecture, we saw that we estimated that the transportation industry accounted for 25% of global energy demand.
Today, we have had a glimpse at the energy use in buildings. We estimate that residential and commercial buildings together account for 20 percent of the global energy demand. Smarter buildings with increased insulation, energy-efficient appliances as well as economical use of household electricity can help bring this down significantly. However, as standards of living in developing countries grow, the number of electrical appliances in each household will continue to grow as well. Will energy efficiency measures help counteract the inevitable increase in household energy use?


